Leetcod hard

Leetcode::problem(42) Trapping Rain Water

Leetcode ps hard

Leetcode::Trapping Rain Water

Link : Leetcode::Trapping Rain Water
level : hard

point

There are n number of bars on each index
Compute how much water it can trap after raining

Design

My way

Well, we can solve this problem by brute force but it takes O(N^2) obviously
If we use sort wisely, we can solve this problem
First of all we sort {height, index}
Then we iterate sorted array from left to right
- It means that we are iterating from the heighst bar to lowest bar
- We are going to manage the section of indices that we already counted
- There is only one section always
While iterating the array, we either enlarge the section or ignore it
- We ignore the index if it is included in the secion, which means it is counted already
- If we haven’t met current index, we enlarge the section and add water amount between the section’s edge and current position

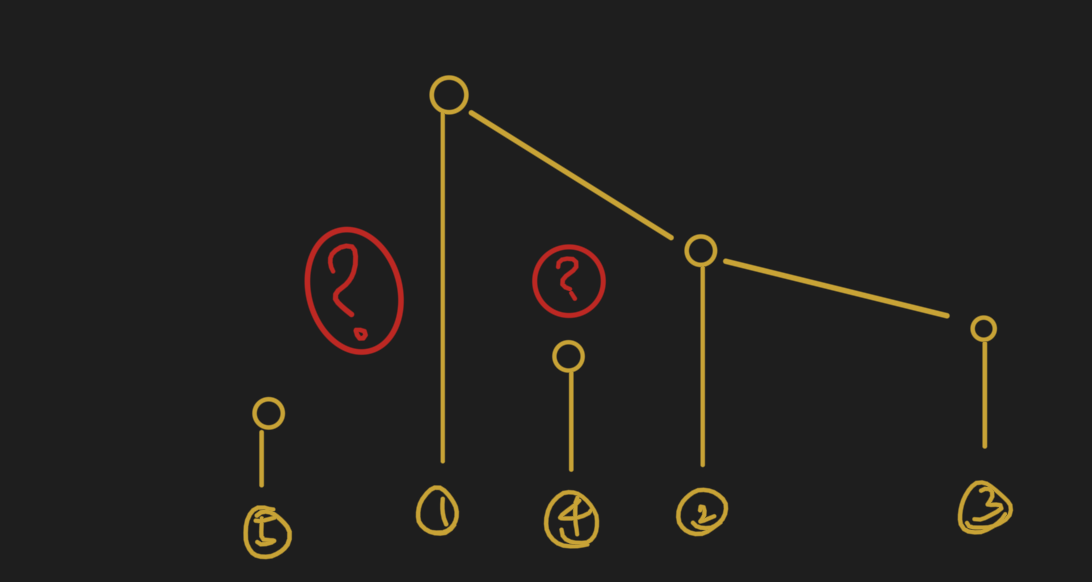
Approach 2 (DP)

From the point of index i, we only need the max height from left side of it and right side of it
Then we would know the smaller one between them, let’s say the smaller one’s index is ‘k’
- For index i, the amount of water would be height[k] - height[i]

Approach 3 (Stack)

This approach is hard to come up but it is useful
We only store index on a stack in a decreasing way of order
While doing that, if we get a height of index that’s going to break the decreasing order (from the stack) we use this index until the last number from the stack is larger than current index, since we need to make the stack in decreasing order
Check below image that I draw

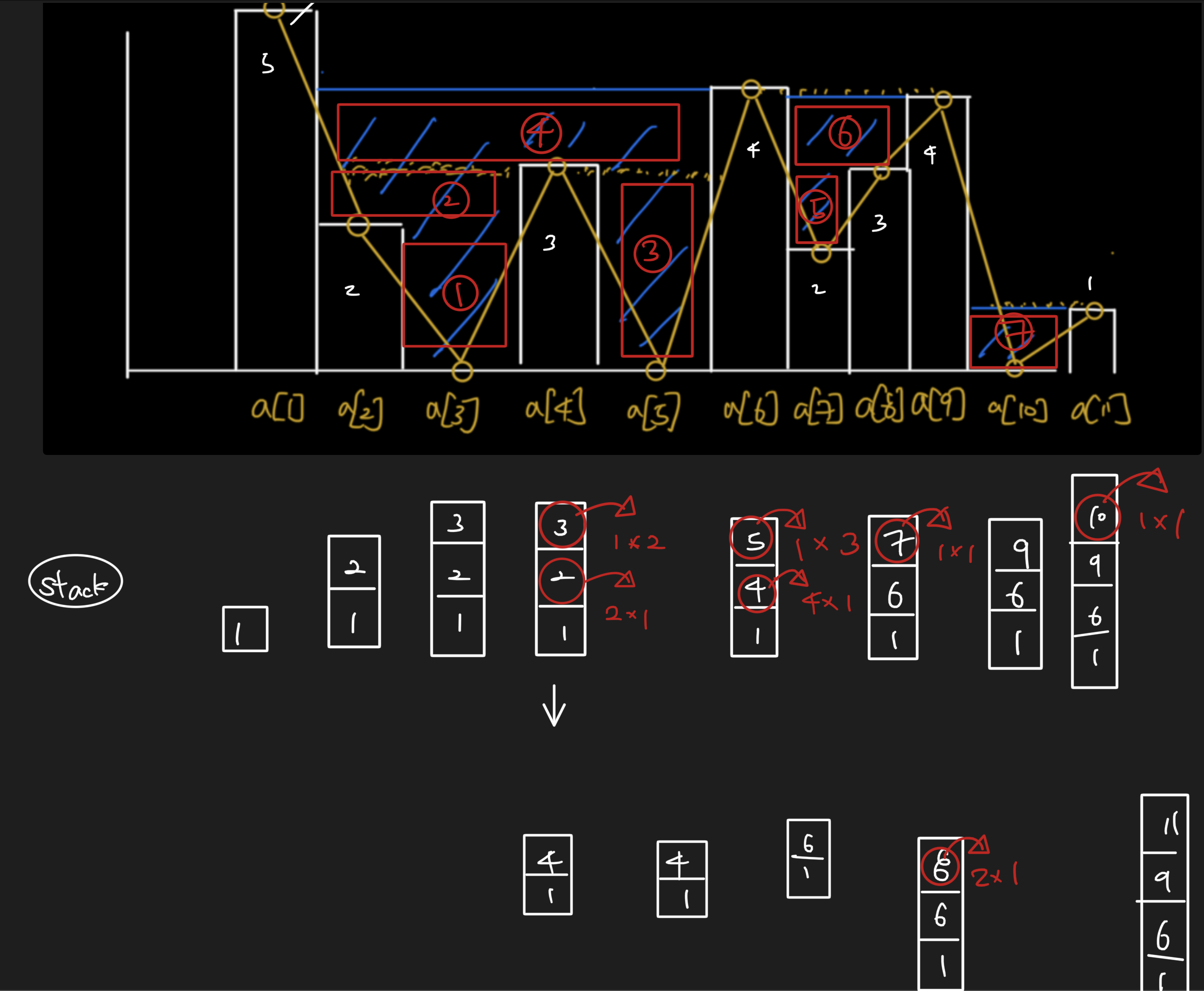
After popping from the stack, we add distance * height of red box to the answer

Big O(time)

My way -> O(NlogN)
Approach 2, 3 -> O(N)

Code

My way

class Solution {
public:
    typedef long long ll;
    int trap(vector<int>& height) {
        int n = (int)height.size();
        vector<pair<int,int> > h2(n);
        vector<int> top(n, 0);

        for(int i = 0; i < n; i++) h2[i] = {height[i], i};

        sort(h2.rbegin(), h2.rend());

        ll sum = 0, le = -1, ri = -1;
        for (int i = 0; i < n; i++) {
            int id = h2[i].second, h = h2[i].first;
            if (le == -1) le = ri = id, top[id] = h;
            else {
                if (id < le || id > ri) {
                    if (id < le) {
                        for(int j = id; j < le; j++) top[j] = h;
                        le = id;
                    } else {
                        for(int j = ri + 1; j <= id; j++) top[j] = h;
                        ri = id;
                    }
                } else {
                    // do nothing
                }
            }
        }
        for(int i = 0; i < n; i++) {
            sum += (top[i] - height[i]);
        }
        return sum;
    }
};

Approach 2

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<int> leftMax(n, 0), rightMax(n, 0);
        leftMax[0] = height[0], rightMax[n-1] = height[n-1];
        for(int i = 1; i < n; i++) leftMax[i] = max(leftMax[i-1], height[i]);
        for(int i = n-2; i >= 0; i--) rightMax[i] = max(rightMax[i+1], height[i]);

        int ans = 0;
        for(int i = 1; i < n -1 ; i++) {
            ans += max( min(leftMax[i-1], rightMax[i+1]) - height[i], 0);
        }
        return ans;
    }
};

Approach 3

class Solution {
public:
    int trap(vector<int>& height) {
        vector<int> stk;
        int ans = 0, current = 0, n = height.size();
        while(current < n) {
            while(!stk.empty() && height[stk.back()] <= height[current]) {
                int top = stk.back();
                stk.pop_back();
                if (stk.empty()) break;

                int dist = current - stk.back() - 1;
                int h = min(height[current], height[stk.back()]) - height[top];
                ans += dist * h;
            }
            stk.push_back(current++);
        }

        return ans;
    }
};