알고리즘 문제해결 전략

Ch.8.12 문제 ID ASYMTILING

종만북

8.12 문제: 비대칭 타일링 ( 문제ID : ASYMTILING, 난이도: 하)

문제 분류 : 동적계획법 (메모이제이션)

내가 시도한 접근 (실패)

좌, 우 대칭의 수를 제한다.
- 좌, 우 대칭인지 확인이 필요하다.
  - n/2을 기준으로 0 1 2 … n-2 n-1 n 순일때 left 와 right의 원소가 같다는 CS적 의미
  - 위의 작업을 진행하기 위해서는 확인하기 위한 매개체 필요 -> vector로 축적
  - tiling(n-1)의 경우 vector에 1을 push
  - tiling(n-2)의 경우 vector에 2를 push
  - 기저사례인 0에 도착했을 때 이를 꺼내서 확인
결론적으로, 예제의 테스트케이스도 답을 도출해내지 못함.

int tiling(int y, vector<int>v) = y열부터 0열까지 놓을 수 있는 블록의 가짓수에서 대칭되는 경우를
                                  제외한 경우의 수를 return 한다.

const int mod = 1000000007;
int n;
int cache[101];
bool isButterfly(vector<int>& v){
    for(int left = 0; (left <= v.size()/2) && (left <= v.size()-left); left++)
        if(v[left] != v[v.size() - left])
            return false;
    return true;
}
int tiling(int y, vector<int>& v){
    if(y <= 2){
        if(v.size() == 0)return 0;
        if(isButterfly(v))return 0;
        else return 1;
    }
    int& ret = cache[y];
    if(ret != -1)return ret;
    ret = 0;
    v.push_back(1);
    ret += (tiling(y-1, v))%mod;
    v.pop_back();
    v.push_back(2);
    ret += (tiling(y-2, v))%mod;
    v.pop_back();
    return ret;
}

책에 제시된 풀이 1

변형된 완전탐색

이 문제처럼 직접 풀어본 문제의 변형된 형태를 만나면, 이 문제를 직접적으로 풀기보다 좀 더 단순화된 문제의 해법을 이용해서 더 쉽게 풀 수 있는 경우가 있습니다.

힌트는 모든 타일리은 대칭이거나 비대칭이라는 데서 옵니다.

이때 모든 타일링은 TILING2 문제에서 센 적이 있습니다.

대칭 타일링의 수를 세는 첫 번째 단계는 n이 짝수인 경우가 홀수인 경우를 각각 나눠보는 것입니다.
n이 홀수인 경우, 타일링 방법이 대칭이기 위해서는 항상 정가운데 있는 세로 타일 하나로 덮어야 합니다.
그리고 왼쪽 절반은 오른쪽 절반과 서로 대칭이어야 합니다. ( 그림 (a))
n이 짝수인 경우, 대칭 타일링에는 두 종류가 있습니다.
(b)와 같이 정가운데 세로줄 둘을 가로 타일로 덮고 나머지 절반이 대칭인 경우와,
(c)처럼 절반으로 나뉜 부분들이 서로 대칭인 경우입니다.

추가적으로, 짝수와 홀수 n을 따로 처리한 부분과, 두 값을 뺀 후 MOD로 나누기 전에 MOD를 미리 더해주는
부분을 눈여겨 보아야 합니다.
tiling()의 반환 값은 경우의 수이기 때문에 결코 음수일 수 없지만, tiling()은 MOD로 나눈 나머지를
반환하기 때문에, 실제 경우의 수가 양수라도 수 루를 뺀 값은 음수일 수 있습니다.

const int MOD = 1000000007;
int n;
int cache[101];
// 2*width 크기의 사각형을 채우는 방법의 수를 MOD로 나눈 나머지를 반환한다.
int tiling(int width){
    // 기저사례 : width가 1이하일 때
    if(width <= 1) return 1;
    // 메모이제이션
    int& ret = cache[width];
    if(ret != -1)return ret;
    return ret = (tiling(width-2) + tiling(width-1)) % MOD;
}

// 2*width 크기의 사각형을 채우는 비대칭 방법의 수를 반환한다.
int asymmetric(int width){
    if(width % 2 == 1)
        return (tiling(width) - tiling(width/2) + MOD) % MOD;
    int ret = tiling(width);
    ret = (ret - tiling(width/2) + MOD) % MOD;
    ret = (ret - tiling(width/2-1) + MOD) % MOD;
    return ret;
}

책에 제시된 풀이 2

직접 비대칭 타일링 수 세기

물론 풀이 1처럼 돌아가지 않고, 직접 비대칭 타일링의 수를 셀 수도 있습니다.

비대칭 타일리의 수를 세는 간단한 방법은 모든 타일링 방법을 만들어 보고 이 중 좌우 대칭이 아닌 것만을 걸러내는 것입니다.

그러나 이런 방법으로는 메모이제이션을 적용할 수 없습니다.

메모이제이션에 과거 조각의 정보를 전부 전달하지 않고서도 문제를 해결할 수 있는 방법은 맨 앞에서부터 타일링 방법을 만들어 가는 것이 아니라 양쪽 끝에서부터 동시에 만들어가는 것입니다.

이와 같은 방법으로는 과거 정보를 알 필요가 없으니, 제 풀이처럼 vector에 저장하고 확인하는 과정이 필요 없게 됩니다.

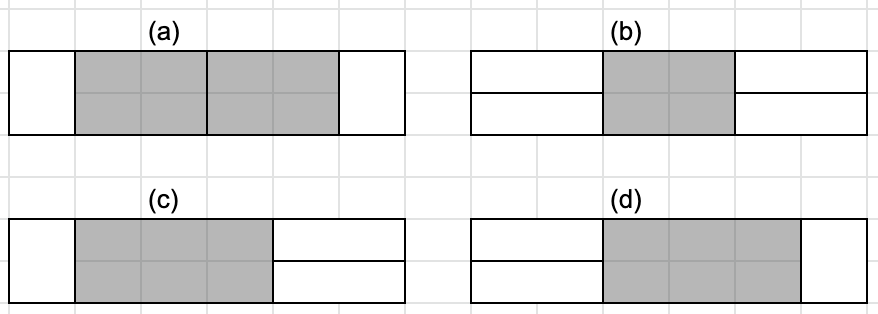
(a),(b) : 가운데 남은 회색 부분을 덮는 방법을 재귀 호출로 찾습니다.
    물론 이 방법은 대칭이 아니어야 합니다. 이 부분까지 좌우 대칭이라면 전체 타일링 방법이 대칭이
    되어버립니다.
(c),(d) : 가운데 남은 회색 부분을 덮는 방법을 찾습니다.
    이 방법은 대칭이라도 상관 없습니다. 회색 부분이 내부적으로 대칭이더라도, 양쪽 끝이 서로 대칭이
    아니므로 전체 타일링 방법은 비대칭이 되기 때문입니다.

int cache2[101];
// 2*width 크기의 사각형을 채우는 비대칭 방법의 수를 반환한다.
int asymmetric2(int width){
    // 기저 사례: 너비가 2 이하인 경우
    if(width <= 2) return 0;
    // 메모이제이션
    int& ret = cache2[width];
    if(ret != -1) return ret;
    ret = asymmetric2(width-2) % MOD; // (a)
    ret = (ret + asymmetric2(width-4)) % MOD; // (b)
    ret = (ret + tiling(width-3)) % MOD; // (c)
    ret = (ret + tiling(width-3)) % MOD; // (d)
    return ret;
}