8.9 문제: Quantization ( 문제ID : QUANTIZE, 난이도: 중)

• 분류 : 동적계획
• 동적계획의 핵심은 점화식을 세우는 것이라고 생각합니다.
  • 점화식을 세우기 위해서는, 각 함수가 하는 역할을 미리 한글로 풀어 써놓고
  • 하나의 함수는 보통 하나의 역할만 하도록 구분 짓는 글쓴이의 문제 접근법에서 배울 점이 매우 많다고 생각합니다.

접근법

기존의 방법

quantize(A) = A에 속한 수를 양자화해서 얻을 수 있는 최소 오차 제곱의 합

• 위와 같은 식의 정의는 최적 부분 조건이 성립하지 않습니다.
  • 사용할 수 있는 숫자의 가짓수에 제한이 있기 때문에 남은 문제를 재귀적으로 해결할 때는 이 함수처럼 지금까지 사용한 숫자들을 무시할 수가 없습니다.

변형된 방법

quantize(A,U) = U가 지금까지 한 번 이상 사용한 숫자들의 집합일 때 A에 속한 수를 양자화해서 얻을 수
있는 최소 오차 제곱의 합

• 위와 같은 방법은 quantize()를 통해 A의 첫 번째 숫자를 어떻게 표현할지를 결정하고 나머지를 재귀 호출해서 해결하게 됩니다.
• 하지만 이런 완전 탐색 코드는 실로 엄청나게 많은 수의 답을 하나하나 만들게 되므로, 사용 불가능하다고 합니다.

답의 형태 제한하기

• 이와 같이 부분 문제의 개수가 너무 많을 때 우리가 시도할 수 있는 방법 중 하나는
• 답이 항상 어떤 구조를 가질 것이라고 예측하고 그것을 강제하는 것입니다.

  주어진 수열을 정렬하면, 같은 숫자로 양자화되는 숫자들은 항상 인접해 있다!
  

• 예를 들어 {1,2,3,4}를 양자화하는데, 최적해가 {2,2,3,2}와 같은 형태일 리는 없다는 것입니다.
• 따라서 이 문제는 이제 주어진 수열을 s개의 묶음으로 나누는 문제가 됩니다.
• 첫 묶음의 크기를 x라고 한다면 이제 나머지 n-x개의 숫자를 s-1개의 묶음으로 나누면 됩니다.
• 이때 나머지 s-1묶음의 오류 합이 최소여야 전체도 최소 오류이기 때문에, 최적 부분 구조 또한 성립한다는 것을 알 수 있습니다.

quantize(from, parts) = min [ minError(from, from + size -1) + quantize(from + size, parts -1) ]
    : from번째 이후의 숫자들을 parts개의 묶음으로 묶을 때, 최소 오류 제곱 합을 반환하는 함수

minError(a,b) : a번째 숫자부터 b번째 숫자까지를 하나의 수로 표현했을 때의 최소 오류를 반환하는 함수

minError()의 구현

minError(a,b)에서 해야하는 일은 크게 두 가지 입니다.
1. 주어진 구간을 어떤 수로 표현해야 할지 결정하기
2. 결정한 수m으로 해당 구간을 표현했을 때 오차를 계산하기

1. 주어진 구간 표현

• 주어진 구간에서 오차를 최소로 만드는 수는 미분을 사용하여 쉽게 찾을 수 있습니다.
• 오차 제곱의 합을 다음과 같이 풀어 써 봅시다.

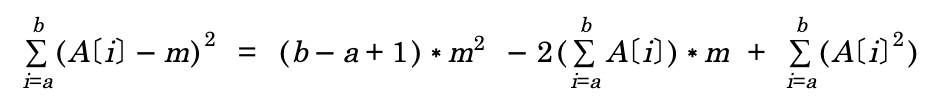
• 이 식은 m에 대한 2차식이고, 2차항의 계수가 양수이므로 미분을 통해 최소점을 구할 수 있습니다.
• m에 대해 미분한 뒤, 0이 되는 점을 다음 식을 풀어서 찾을 수 있습니다.

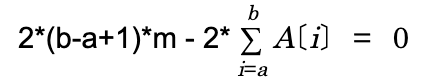
• 위 식의 답이 되는 m은 다음과 같습니다.

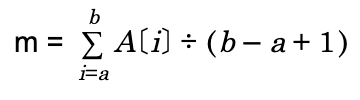
• 즉 모든 값의 평균을 사용하면 오차를 최소화할 수 있다는 사실을 알 수 있습니다.
• 우리는 정수만을 사용할 수 있으므로 평균에 가장 가까운 정수, 곧 반올림한 값을 사용합니다.
• 주어진 구간의 평균을 계산하는 작업은 O(n)의 시간이 걸리지만, 17장에서 소개하는 기법인 부분 합을 이용해 다음과 같이 O(1)에 계산할 수 있습니다.
• 우선 다음 정의에 따라 A의 부분 합을 계산합니다.

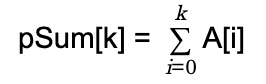
• 이식을 이용하면 A[a]부터 A[b]까지의 합을 다음과 같이 구할 수 있습니다.

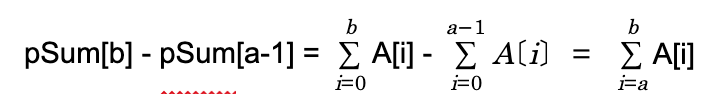
2. 오차 계산하기

• 오차 제곱은 아래 식을 부분합을 이용하여 O(1)에 계산하는 것이 가능합니다.

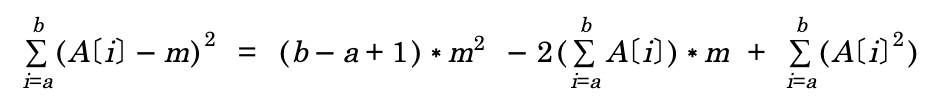
• 이상의 방법에 의해 minError(a,b)를 O(1)에 계산할 수 있습니다.
• 따라서 알고리즘의 전체 시간 복잡도는 부분 문제의 수 O(ns)에 각 부분 문제의 답을 계산하는 데 드는 시간 O(n)을 곱한 O(n^2s)가 됩니다.
• 코드 참조
  • sort(A, A+n); 처럼 일반 배열도 sorting 이 가능하다.
  • int(0.5 + (double)sum / (hi-lo+1)) 을 통해 반올림을 사용하였다.

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int inf = 987654321;
// A[]: 양자화해야 할 수열, 정렬한 상태
// pSum[]: A[]의 부분합을 저장한다. pSum[i]는 A[0] .. A[i]의 합
// pSqSum[]: A[]제곱의 부분합을 저장한다. pSqSum[i]는 A[0]^2 .. A[i]^2의 합
int n, m;
int A[101], pSum[101], pSqSum[101];
// A를 정렬하고 각 부분합을 계산한다.
void precalc(){
    sort(A, A+n);
    pSum[0] = A[0];
    pSqSum[0] = A[0] * A[0];
    for(int i = 1; i < n; i++){
        pSum[i] = pSum[i-1] + A[i];
        pSqSum[i] = pSqSum[i-1] + A[i]*A[i];
    }
}
// A[lo]..A[hi] 구간을 하나의 숫자로 표현할 때 최소 오차 합을 계산한다.
int minError(int lo, int hi){
    // 부분합을 이용해 A[lo] ~ A[hi]까지의 합을 구한다.
    int sum = pSum[hi] - (lo == 0 ? 0 : pSum[lo-1]);
    int sqSum = pSqSum[hi] - (lo == 0 ? 0 : pSqSum[lo-1]);
    // 평균을 반올림한 값으로 이 수들을 표현한다.
    int m = int(0.5 + (double)sum / (hi - lo + 1));
    int ret = sqSum -2 * m * sum + m * m * (hi - lo + 1);
    return ret;
}

int cache[101][11];
int quantize(int from, int parts){
    // 기저 사례: 모든 숫자를 다 양자화 했을 때
    if(from == n)return 0;
    // 기저 사례: 숫자는 아직 남았는데 더 묶을 수 없을 때 아주 큰 값을 반환한다.
    if(parts == 0)return inf;
    int& ret = cache[from][parts];
    if(ret != -1)return ret;
    ret = inf;
    // 조각의 길이를 변화시켜 가며 최소치를 찾는다.
    for(int partSize = 1; from + partSize <= n; partSize++)
        ret = min(ret, minError(from, from + partSize -1) + quantize(from + partSize, parts - 1));
    return ret;
}